sun cloud

용어 소개

이번 강의에서는 Heap과 Tree에 대해 배울 예정입니다.

본격적인 내용 진행에 앞서 용어들을 간단히 살펴보겠습니다.

image

(출처: 트리(그래프) - 나무위키)

위의 그림은 Tree를 나타내고 있습니다.(일반적인 나무 모양을 뒤집어서 생각하시면 됩니다)

가계도처럼 노드를 나무 형태로 연결한 구조를 트리라고 합니다. 트리에 있는 각각의 요소는 노드입니다. 위 사진에서처럼 노드는 부모, 자식 형태로 이어집니다.

  • root: 가장 중요한 트리의 시작 부분입니다. 트리는 항상 root를 통해 탐색하게 됩니다.

  • leaf/leaves: 자식이 딸려있지 않은 말단 부분입니다.

  • edge: 두 노드를 연결하는 선입니다. 뿌리로부터의 간선의 수에 따라 level을 나눕니다.

  • siblings: 동일한 부모를 갖는 형제 노드들을 말합니다.

  • level: 깊이를 나타내는 노드의 집합입니다. 뿌리부터 시작합니다.



Heap

힙은 트리와 비슷한 구조를 가지는데, 최대 힙과 최소 힙 두 가지 종류가 있습니다.

  • 최대 힙(Max Heap): 부모 노드 > 자식 노드

  • 최소 힙(Min Heap): 부모 노드 < 자식 노드

image

(왼쪽: 최대 힙 - 숫자 12를 부모로 갖는 level3에서 노드가 꽉 차야 합니다, 오른쪽: 최소 힙)

힙은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기반으로 한 자료구조입니다. (완전이진트리란, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있는 트리)

그리고 최대 힙에서는 노드의 개수를 통해 높이를 알 수 있습니다.

image

image

(노드 개수(n)을 이용해 level, height과 log(n+1)-1의 값이 같다는 것을 알 수 있음)



Add, Remove

앞서 힙에 대해 설명할 때 규칙에 따라 부모 노드와 자식 노드의 위치가 정해진다고 했습니다. 그래서 새로운 데이터를 추가하거나 제거할 때에도 힙의 규칙을 지켜야 합니다.

최대 힙이면 부모 노드가 자식 노드보다 커야 하고 최소 힙은 자식 노드가 부모 노드보다 커야 합니다.

 

노드 추가(Trickle Up)

image

그림과 같이 최대 힙이 있을 때, 새로운 노드로 27을 추가하려고 합니다.

그런데 27은 부모 노드인 10보다 크기 때문에 규칙을 위반하게 되겠죠.

그래서 문제를 해결하기 위해 10과 27의 위치를 바꾸면, 다시 부모 노드와 값을 비교해서 규칙을 지키도록 하면 됩니다.

 

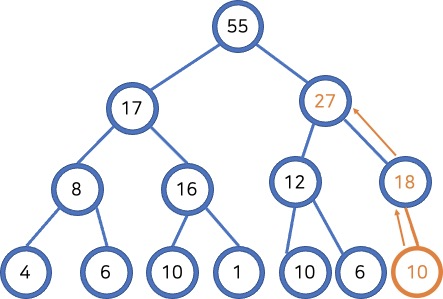
  1. 비어있는 공간에 노드를 추가
  2. 부모 노드보다 큰 숫자인지 확인하고 만약 그렇다면 두 노드를 교환


추가를 알아봤는데, 제거는 어떻게 하면 될까요?

힙에서의 제거는 특정 요소를 지정할 수 없고, 항상 루트 요소를 제거 합니다.

루트를 제거한 뒤에는 규칙을 준수하며 빈 자리를 메꾸면 되겠습니다.

노드 제거(Trickle Down)

 

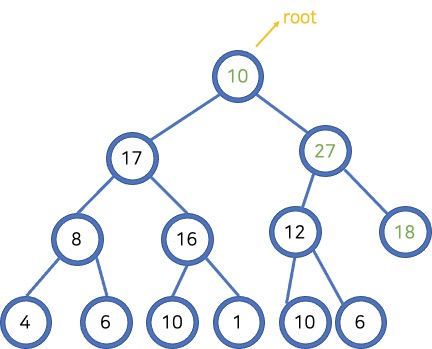
  1. 루트 제거
  2. 트리의 마지막 요소를 루트에 삽입
  3. 루트에서 시작해 두 자식 중 큰 노드와 바꿔 힙 규칙 준수



TrickleUp Method

힙은 완전이진트리이기 때문에 노드의 위치 다음과 같은 성질을 가집니다.

인덱스는 0부터 시작하며 root - left - right 순으로 지정하면 아래의 식을 만족합니다 children: 2 * parent + 1 or 2 * parent + 2 parent: floor((child-1)/2)

image

 

이 성질을 이용하여 노드 추가 과정을 코드로 작성하면 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

int lastposition; // 루트로부터 떨어진 거리, 즉 요소를 어디까지 넣었는지 기록
E[] array = (E[]) new Object[size];
public void add(E obj){
    array[++lastposition] = obj; // 1. 노드 추가
    trickleup(lastposition); // 2. 규칙 준수 확인
}
public void trickleup(int position){
    if (position == 0)
        return;
    int parent = (int) Math.floor((position-1)/2)
    if (((Comparable<E>) array[position]).compareTo(array.parent) > 0) {
        swap(position, parent);
        trickleup(parent);
    }
}
public void swap(int from, int to){
    E tmp = array[from];
    array[from] = array[to];
    array[to] = tmp;
}


TrickleDown Method

힙에서 제거는 루트의 제거를 의미한다고 설명드렸습니다.

루트를 제거한 뒤에도 규칙을 만족하기 위해서는 힙에 있는 마지막 요소로 빈 구멍을 메우고, 자식 노드와 비교해서 교체하는 작업을 반복하면 됩니다. 작업이 종료되는 기준은 배열의 길이(lastposition)보다 2*parent+1, 2*parent+2의 결과값이 큰 경우 종료하게 됩니다.(다만, 자식이 하나만 존재하는 경우도 고려해야 합니다)

루트 제거 과정을 코드로 작성하면 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

public E remove(){
    E tmp = array[0]; // 루트를 바로 제거하지 않고 스왑함으로써 remove 반복 시 오름차순으 정렬
    swap(0, lastposition--); // 스왑 이후 lastposition을 감소시켜 배열에서 제거
    trickleDown(0);
    return tmp;
}
public void trickleDown(int parent){
    int left = 2*parent + 1;
    int right = 2*parent + 2;
    // 왼쪽 자식이 마지막 요소인 경우
    if (left==lastposition && 
            (((Comparable<E>)array[parent]).compareTo(array[left]) < 0){
        swap(parent, left)
        return;
    }
    // 오른쪽 자식이 마지막 요소인 경우
    if (right==lastposition && 
            (((Comparable<E>)array[parent]).compareTo(array[right]) < 0){
        swap(parent, right)
        return;
    }
    // 자식이 마지막 요소와 같거나 큰 경우
    if (left >= lastposition || right >= lastposition)
        return;
    // 왼쪽 자식이 클 때
    if (array[left] > array[right] && array[parent] < array[left]) {
        swap(parent, left);
        trickleDown(left);
    }
    // 오른쪽 자식이 클 때
    else if (array[parent] < array[right]){
        swap(parent, right);
        trickleDown(right);
    }
}



Sorting

힙 규칙에 맞게 숫자의 순서를 정렬하는 힙 정렬 알고리즘을 살펴보겠습니다.

임의의 숫자들을 나열한 뒤 힙 규칙에 맞게 TrickleDown을 반복하면 숫자가 정렬됩니다.(루트 제거 시 바로 제거하지 않고, swap을 사용한 이유)

image

(root가 22였던 최대 힙에서 TrickleDown을 실행했을 때 내부적으로 동작하는 첫 번째 과정. 22를 바로 제거하지 않고, 마지막 요소와 swap한 뒤 연결 해제)

image

image

위 과정을 반복하면 정렬이 이뤄집니다.

  1. 22 | 17 | 19 | 12 | 15 | 11 | 7 | 6 | 9 | 10 | 5

  2. 5 | 17 | 19 | 12 | 15 | 11 | 7 | 6 | 9 | 10 | 22(X)

  3. 19 | 17 | 11 | 12 | 15 | 5 | 7 | 6 | 9 | 10 | 22(X)

  4. 10 | 17 | 11 | 12 | 15 | 5 | 7 | 6 | 9 | 19(X) | 22(X)

  5. 17 | 15 | 11 | 12 | 10 | 5 | 7 | 6 | 9 | 19(X) | 22(X)

  6. 9 | 15 | 11 | 12 | 10 | 5 | 7 | 6 | 17(X) | 19(X) | 22(X)

  7. …

  8. 5 | 6(X) | 7(X) | 9(X) | 10(X) | 11(X) | 12(X) | 15(X) | 17(X) | 19(X) | 22(X)

힙 정렬 알고리즘은 두 수를 비교해서 하나를 고르기 때문에 O(nlogn)의 시간 복잡도를 가집니다.

또한, 힙 정렬은 숫자들의 순서를 바꿔 정렬하기 때문에 데이터의 복사본을 만들 필요가 없다는 장점이 있습니다.



참고

자바로 구현하고 배우는 자료구조 > 4.힙(Heap) & 트리(Tree) : 부스트코스

맨 위로 이동하기

DataStructure 카테고리 내 다른 글 보러가기

댓글남기기

참고